[논문 리뷰] (2009, UAI) BPR: Bayesian Personalized Ranking from Implicit Feedback
먼저 본 논문을 리뷰하기 전에 Loss를 계산하는 방법인 point-wise, pair-wise, list-wise에 대하여 간단하게 설명하려고 한다. 본 개념을 알고 들어가면 좋은 이유는 BPR이 pair-wise 방식으로 loss를 계산하는 방법이기 때문이다.
우선 point-wise는 loss를 계산할 때 한번에 1개의 아이템을 고려하는 방식으로, 간단하게 말하며 user가 item을 사용할 확률 값을 구하는 방식이라고 할 수 있다. 예를 들어 positive item과 negative item이 존재한다고 할 때, 우리는 BCE Loss를 사용하여 positive item을 선택할 확률은 1에 가깝게, negative item을 선택할 확률을 0에 가깝게 독립적으로 loss를 계산하여 각 아이템을 사용할 획률을 최적화 하게 된다. 그 후 전체 아이템에 대한 확률 값을 계산한 후 정렬하여 아이템의 순위를 매기게되는데, 이러한 방식이 point-wise라고 할 수 있다.
pair-wise는 Loss를 계산할 때 한번에 2개의 아이템을 고려하는 방식으로, 간단하게 말하면 positive item과 negative item이 주어졌을 때 positive item과 negative item을 loss 계산할 때 함께 사용하여 item에 대한 순위를 고려하는 것이다. 즉 pair-wise는 아이템의 Rank를 고려하여 모델을 학습시키는 방식이라고 할 수 있다.
list-wise는 Loss를 계산할 때 한번에 3개 이상의 아이템을 고려하는 방식으로, 간단하게 말하면 pair-wise의 확장판이라고 할 수 있다. item list가 주어졌을 때, item list 모두를 가지고 loss를 계산하여 item list 내에서 순위를 매기게 된다. 즉 list-wise는 pair-wise와 똑같이 아이템의 Rank를 고려하여 모델을 학습시키는 방식이지만, 고려하는 item의 수가 더 많다는 측면에서 다르다고 할 수 있다.
Recommender System
본 논문은 다양한 추천 주제 중, collaborative filtering에 관한 내용을 다루고 있으며, 구체적으로 optimization에 관한 내용이다.
Abstract
해당 논문은 ‘클릭’이나 ‘구매’와 같은 implicit-feedback 하에서의 추천 문제를 다룬다. 여기서 추천이란 user가 선호할 만한 item목록(personalized ranking)을 예측하는 것을 말한다. Matrix Factorization(MF)과 k-nearest-neighbor(kNN)는 personalized ranking을 구하는 대표적인 방법이다. 하지만 기존의 optimization 기법들은 모두 ranking 을 고려하지 않는 방식으로, 본 논문은 베이지안 추론에 기반한 optimization 기법(BPR-Opt)을 제시해, item들에 대한 user의 선호 강도를 반영할 수 있도록 하였다. 나아가 이를 MF와 kNN에 적용한 결과, 기존의 것보다 우수함을 증명하였다.
1. Introduction
본 논문은 개인화된 아이템 추천에 초점이 맞춰져 있다(개인화된 아이템 추천을 위해서는 아이템의 순위를 매기는 것이 중요함)
현실에는 Explicit feedback(평점 등) 보다 Implicit feedback(웹 로그, 클릭 등)이 더 수집하기 용이(인터넷에 접속만하면 log가 남기 때문에 자동으로 수집이 가능함)하고 그 양도 훨씬 많기 때문에 본 논문은 Implicit feedback를 활용하는 방법에 중점을 두고 있다.
베이지안 추론(maximum a posteriori, MAP)에 기반한 optimization 기법 (BPR-Opt)을 제시한다. 나아가 이것이 ROC 커브 아래의 면적인 AUC(area under curve)를 최대화 하는 문제와 동치임을 보인다.
BPR-Opt를 최대화 하기 위한 알고리즘(LEARN BPR)을 제안한다.
LEARN BPR을 MF, kNN에 적용하는 법을 보인다.
BPR-Opt가 기타 다른 optimization 기법보다 성능이 우수함을 보인다.
2. Related Work
point-wise를 사용하는 모델은 오직 1개의 아이템만을 고려하여 모델이 학습하기 때문에 오직 1개의 랭킹만을 고려할 수 있다, 이러한 방식은 비개인화된 방식이라고 말할 수 있다
따라서 본 논문에서 제안하는 BPR-Opt을 사용하여 아이템의 랭킹을 고려할 수 있기 때문에, 개인화된 추천이 가능하다고 말하고 있다.
3. Personalized Ranking (본 논문의 핵심)
Personalized ranking을 한다는것은 각각의 user에 대해서 그들이 좋아할만한 item들을 줄세워서 상위 몇개를 추천 해주는 것이다. 여기서 주의 할 사항은 대부분의 정보는 implicit 하기 때문에 explicit data를 분석할 때와는 다른 접근이 필요하다. 핵심적으로는 negative feedback이 없는것인데, 간단한 예를 들어보자.
내가 쿠팡에서 초콜렛을 사 먹은 기록이 없다는 것은, 내가 초콜렛을 싫어할수도 있는거고, 그냥 단순히 살 생각을 안해서 안 샀을수도 있는 것이다. explicit data였다면 내가 초콜렛을 사서 별점을 1점을 줬으면 싫어하는 것이고, 아직 산 적이 없으면 그냥 단순히 산 적이 없는 것이다. 이렇게 호 불호에 대한 표시가 명확한 explicit data와는 달리, implicit data는 분석이 더 어렵고, 복잡하다. 하지만 당연히 더 중요하다.
3.1 Formalization
: 모든 user들의 집합
: 모든 item들의 집합
: 반응이 있는 implicit feedback 들,
: 아이템들의 순위를 비교하는 연산자,
가 을 보다 좋아한다면 로 표현한다. 이 연산자는 아래 3가지 특성을 만족한다.
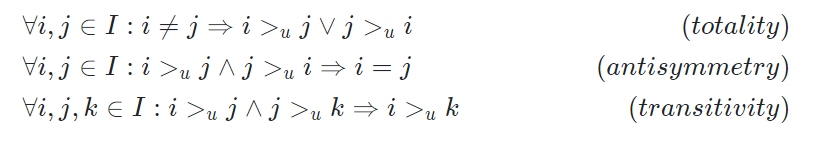
풀어서 설명하면
- totality 는 서로 다른 어떠한 아이템 에 대해서 든, 든 둘중 하나의 방식으로 가 정의될 수 있음을 의미한다.
- antisymmetry 는 순서가 있음을 의미한다. 에서 의 순서가 바뀌면 의미가 달라진다.
- transitivity 는 를 보다 좋아하고 를 보다 좋아하면 를 보다 좋아한다는 뜻이다.
마지막으로 편의상 아래 두 집합을 정의한다.
: user 가 평가한 아이템들의 집합
: item 를 구매한 유저들의 집합
3.2 Analysis of the problem setting
implicit feedback dataset에서 0 (평가되지 않은 항목)을 처리하는건 굉장히 중요하다. 여러가지 방법이 있을 수 있다. 몇가지 예시를 들어보도록 하자.
- 0을 무시해버리기
가장 쉬운 방법은 그냥 0을 무시해버리고 학습하는 경우다. 이렇게 0을 배제하면 positive feedback만 남기 때문에 당연히 문제가 생긴다.
- 0들도 모두 학습해보기
위에 설명한것처럼 0을 무시하면 안되니까 0을 모두 학습하면 될까? 또 문제가 생긴다. 우리가 예측하고자 하는것은 빈칸 0에 대해 유저가 몇점을 줄지 예측하고 싶은 것인데, 0을 이미 부정적인것으로 학습한 꼴이 된다. 추가적으로 과적합 문제도 발생할 수 있다. 아래는 이런 경우 design matrix가 어떻게 구성되는지 보여준다.

여기서 ‘+’는 관측된 데이터, ‘?’는 관측되지 않은 데이터다. 이 경우 학습데이터는 관측된 데이터는 1로, 관측되지 않은 데이터는 0으로 표기되며 ,1은 선호 0은 비선호를 의미한다. 하지만 이런식의 디자인은 향후 user가 선호할지도 모르는 item들도 0으로 표기되는 문제가 있다. 예를 들어 데이터가 ‘구매 여부’라 한다면 user가 특정 item을 구매할 확률을 예측하는 문제를 풀게 되는데, 이때 실제로 user가 구매할지도 모르는 item들도 0으로 예측되는 문제가 생기는 것이다.

이 세팅은 다음과 같이 3가지 가정을 따른다.
- 이미 구매 한 아이템은 구매하지 않은 아이템보다 선호도가 높다.
- 구매 한 아이템 끼리의 선호는 구분할 수 없다.
- 구매하지 않은 아이템 끼리의 선호는 구분할 수 없다.
이제 우리는 이 차이만을 가지고 학습을 진행할 것이기 때문에, 이를 통해 새로 데이터 셋을 만든다. 이렇게 만든 데이터 셋을 라고 한다.
로 나타낼 수 있는데, 설명하자면 user 가 item 를 item 보다 더 좋아한다는 뜻이다.
이와 같이 ranking을 기반으로 한 문제정의 방식은 다음과 같은 특징이 있다.
- 관측되지 않은 item에도 정보를 부여해 간접적으로 학습시킬 수 있도록 한다. (기존 방식처럼 모두 0으로 간주하는 것보다 나은 결과를 줌)
- 관측되지 않은 item들에 대해서도 순서를 메길 수 있다. 즉 기존 방식은 모두 0으로 예측되어 순서를 메길 수 없었던 것과 달리, ranking을 학습함으로써 이를 추론할 수 있도록 한다. 이때 가 학습 데이터로 사용된다.
4. Bayesian Personalized Ranking (BPR)
앞으로 우리가 할 것을 정리해보면 아래와 같다.
- 새로운 방식인 BPR-OPT를 이용해 최적화 하는 방법 설명
- 를 알아야한다.
- 이 과정이 ROC의 AUC와 유사함을 보인다. (흐름상 중요하지 않다고 판단해 포스팅에선 생략한다.)
- 더 효과적인 수렴을 위한 LEARN BPR 알고리즘을 제안
- 이 방법을 MF, kNN에 적용
4.1 BPR Optimization Criterion
추천 시스템의 대표 주자인 MF와 kNN 방식이 각 유저 에 대해서 item 의 랭킹을 매기는 상황에서 필요한 것은 각각 아래와 같다.
- MF : Latent factor 찾기
- kNN : similarity matrix 찾기
즉 MF의 경우는 Latent factor가, kNN에 대해서는 similarity matrix가 parameter 가 된다.
아무튼 모델들에 따라서 다른데, 주어진 에 대해서 를 최대화 하면 된다. 여기서 Bayesian 을 이용한다.
MF의 경우를 예시로 들어 조금 풀어서 설명을 해보자. 3.1 Formalization을 보면 새로운 연산자 가 정의되었고, 이를 통해 학습을 할 계획이다. MF에서 학습의 대상은 각각의 user와 item들에 대한 Latent factor들 이다. 즉 우리는 주어진 를 가장 잘 설명할 가능성이 높은 를 찾는것이 목표고, 이것을 수식으로 나타내보면 이다.
와 각각 하나씩 구해보도록 한다.
먼저 를 정리해보자.
유저, 아이템끼리 모두 독립이면 아래처럼 정리 된다.
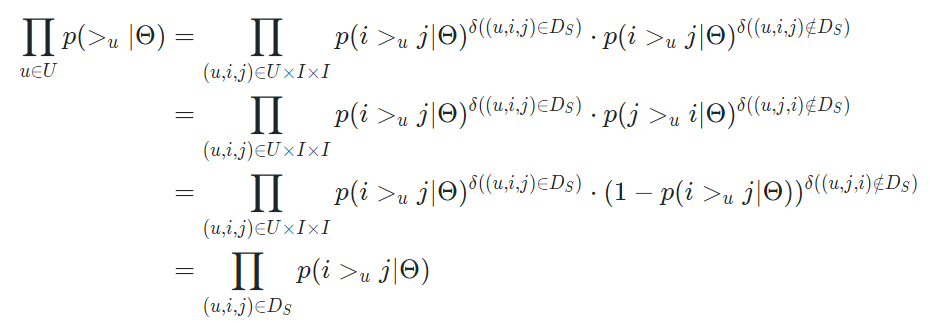
정리한 결과를 보면 를 수치화 해야한다는 것을 알 수 있다. 는 결국 확률이고, 0~1 사이의 값을 갖는다. 이를 가장 잘 나타내는 것은 우리가 잘 아는 sigmoid 함수다. 따라서 해당 값을 아래처럼 정의한다.
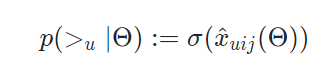
이렇게 임의의 새로운 함수 에 대해서 그냥 시그모이드로 나타내버렸다. 가 의 관계에 대한 연산자이므로 의미상 문제는 없다. 이제 임의의 함수인 를 알아내는것이 새로운 목표가 됐다. 참고로, 앞으로의 수식 전개에서 편의상 를 로 를 생략해서 사용한다.
위에서는 를 로 바꾸어 나타내는 과정을 진행했다.
이제 나머지 하나인 를 수치화 해보도록 한다.
수식을 진행하기에 앞서 몇가지 가정을 한다. 는 우리가 구하고자 하는 parameter다. 이게 어떻게 분포되어 있는지 알 수 없으므로, 일반적으로 그냥 Normal distribution이나 Uniform distribution을 따른다고 가정한다고 한다. 이 논문에서는 아래와 같은 정규분포를 따른다고 가정했다. 계산의 용이성을 위해 variance-covariance matrix도 간소화 했다.

이제 이것을 이용해서 를 구해보자.

앞선 두가지 단계를 통해서 를 계산할 수 있게 됐다. 이제 이를 통해 BPR-OPT를 정의할 수 있다.

이제 를 따로 구해보면 아래와 같다.

가 모두 상수이므로 새로운 상수 로 나타낼 수 있다. 여기서 우리의 목적은 의 정확한 값을 구하는 것이 아닌, 최대화를 하는 것이다. 따라서 은 무시할 수 있다. 또한 도 하나의 hyperparameter일 뿐이므로 를 아래처럼 나타낸다.

결과적으로 식을 정리하면 논문과 동일한 결과를 얻을 수 있다.

4.2 BPR Learning Algorithm
이제 BPR-OPT를 구했으니 에 대해 미분해서 gradient descent 를 사용하면 된다. SGD를 하는게 일반적이다.

이를 해결하기 위한 방법이 LEARN BPR 이다. 특별한건 아니고 그냥 uniform distribution처럼 뽑는것이다. 원래는 데이터 셋에 가 너무 많아 랜덤 추출을 할 때 많이 나오는것이 문제였는데, 개수에 따라서 뽑는게 아니라 동일 확률이라고 하고 뽑으면 된다. 또한 이 논문에서는 여기에 bootstrap sampling 방법도 적용했는데, 두가지 이유가 있다.
- 데이터가 충분히 많기 때문에 적은 양으로 수렴이 가능하다.
- 따라서 수렴 했으면 그냥 중간에 꺼버릴 수 있으면 좋다.

4.3 Learning models with BPR
이제 앞에서 나온 내용 BPR-OPT 을 LEARN BPR을 통해 어떻게 하는지 MF랑 kNN에 적용해보도록 한다.

이 식으로 재 정의한다. 왜냐면 대부분의 기존 model은 3개를 다 보는게 아니라 간 관계만 보기 때문이다.
다시한번 강조하지만, 이 논문은 점수를 매기는데 초점을 맞추던 원래 방안을 차이를 이용해서 rank를 매기는것으로 변경한다. 논문에서는 두가지 방법을 모두 다뤘지만, 포스팅은 MF에 대해서만 설명하도록 하겠다.
4.3.1 Matrix Factorization
MF는 기본적으로 두 행렬의 곱으로 나타낸다. 그러면 는 두 행렬 다. 그러면 이것들에 대해서 미분 한 값을 구할 수 있으면 된다.
: 예측하고자 하는 값들
: user들의 latent factors,
: item들의 latent factors,
는 에서의 행벡터다.
따라서 하나의 value 는 아래와 같다.

4.2 BPR Learning Algorithm를 보면 결국 우리가 해야 할 것은 를 계산하는 것임을 알 수 있다. 4.3 Learning models with BPR에서 라고 재정의 했음을 떠올리면 쉽게 계산할 수 있다. 결과는 아래와 같다.

추가적으로 regularization constant도 세개 썼다. 이제 계산에 필요한 모든 수치를 구할 수 있다.
5. Conclusion
기존에 점수에 초점을 맞춘 모델들에 대해서 랭킹에 초점을 맞춰서 초기화하니까 더 좋다!
이 과정에서 implicit feedback data를 잘 처리해줬다.
- 이미 구매 한 아이템은 구매하지 않은 아이템보다 선호도가 높다.
- 나머지 경우는 알 수 없다.
최적화 과정에서 Bayesian을 사용했다. 이름이 BPR인 이유다.
이 BPR을 최적화 하기 위해 LEARN-BPR이라는 알고리즘을 제시했다.
Code Review
References
1. https://arxiv.org/ftp/arxiv/papers/1205/1205.2618.pdf
2. https://cseweb.ucsd.edu/classes/fa17/cse291-b/reading/04781145.pdf
3. https://cornac.preferred.ai/