Linear Regression : y = Wx + b로 표시되는 선형식으로 x와y 사이의 관계를 찾는 모델.
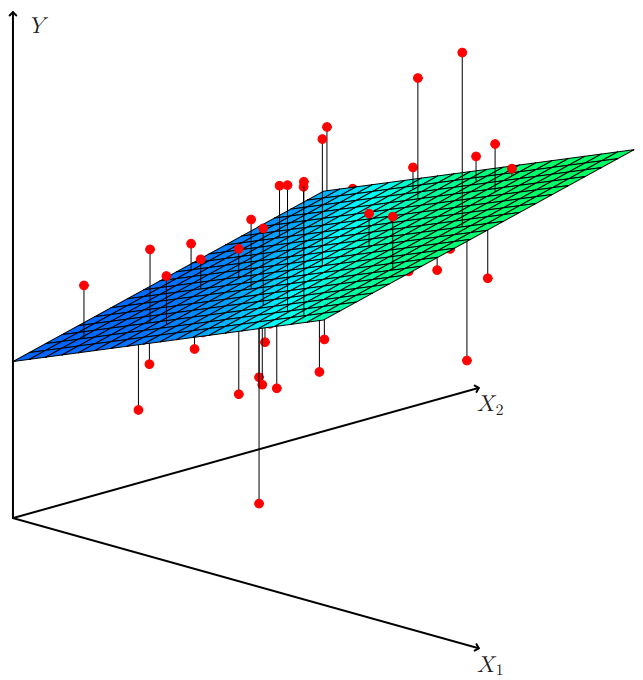
Linear regression은 하나의 선형식으로 X와 y사이의 관계를 찾아내는 방법입니다
분류와 다르게, 회귀 모델은 선형식의 계산 결과 자체가 예측 값입니다.
Go Detail
- y = Wx + b 의 식을 자세히 들여다보면, 다음과 같이 표시할 수 있습니다. → y = w_1 * x_1 + w_2 * x_2 + ... + w_n * x_n + b
- 분류와 접근 방식이 동일하기 때문에, 겹치는 설명은 스킵하겠습니다.
- Linear Classifier처럼 처음에는 랜덤 값을 가지는 w_i들을 가지고 예측을 수행합니다.
- 임의의 값 y_i 가 나왔습니다. 이 예측값은 (정말 운이 좋은 경우를 제외하고) 실제 값과 많이 동떨어져 있을 것입니다.
- 예측 값이 실제 값과 가까워지려면 파라미터들(w, b)을 업데이트 해야합니다.

- 이 때 Gradient Descent algorithm이 사용되어 w, b를 업데이트 해줍니다.
- 업데이트가 되는 방향은 주어진 Loss function의 최소가 되는 지점으로 향하는 방향입니다.
- Linear Regression의 최적화 함수(MSE)가 convex하기 때문에, 주어진 데이터들에서는 항상 optimal solution을 찾을 수 있습니다
- 물론, 이게 최고의 solution이라니느 얘기는 아니고 Linear Regression이 할 수 있는 best case는 항상 찾을 수 있다는 얘기 입니다.(Gradient Descent algorithm으로)
- 회귀에서 가장 많이 사용하는 Loss function은 MSE(Mean Squard Error)입니다.

- 즉, 모델의 예측값이 실제값에 점점 가까워지게 학습이 됩니다. → 전체적으로 Loss의 평균이 작아지는 방향으로 학습이 진행됩니다.
- MSE를 사용하면 차이가 큰 데이터가 있는 경우 Loss가 더 크게 나오기 때문에. outlier 같은 데이터가 있다면 미리 제거를 해주거나 아니면 보정을 해주는 것이 필요합니다.
- 따라서, Linear regression도 역시 파라미터 W와 b를 찾는 문제가 되며, 적절한 파라미터를 찾았을 때 데이터를 잘 파악하는 선형식을 찾을 수 있게 됩니다.
- Linear Regression은 두 가지의 큰 장점이 있습니다
- 통계적으로 설명 가능한 이론이 많습니다. (설명 도구가 많다.)
- interpretability가 있다.(설명 가능하다) → 수식 자체가 선형식이기 때문에, 직접계산을 해서 예측값이 왜 나오는지 설명이 가능하다
- Linear model 자체가 가지는 simplicity 때문에, general한 모델이 나오는 편입니다. → 오히려 복잡한 모델들 보다 예측력이 더 뛰어납니다!
반응형
'Machine_Learning > 이론' 카테고리의 다른 글
| Regression-04. Model 3 : XGBoost (0) | 2022.11.08 |
|---|---|
| Regression-03. Model 2 : Lasso, Ridge (0) | 2022.11.08 |
| Regression-01. 회귀의 정의 (0) | 2022.11.08 |
| Classification-05. Model 4: Random Forest (0) | 2022.11.07 |
| Classification-04. Model 3 : Decision Tree (0) | 2022.11.04 |



